机器学习 & 深度学习纯小白入门(PyTorch)
前置知识:Python 编程
1. 引言
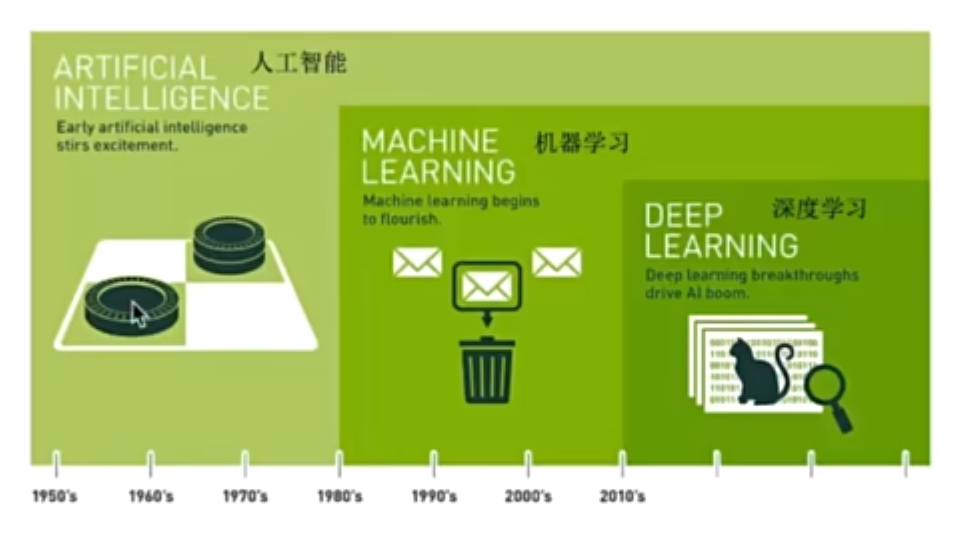
1.1 机器学习是什么?
机器学习是从数据中自动分析获得模型,并利用模型对未知数据进行预测。
比如说我们需要根据一张图片来分辨这张图片到底是猫还是狗:

我们就需要从大量的猫和狗的图片(即数据集)中,辨别猫和狗的规律(自动分析获得模型),从而使得机器具有识别猫和狗的能力。
数据集的组成结构如下:
特征值:描述样本属性的输入变量,用于预测或分类的原始数据。
目标值(标签):模型需要预测或分类的输出结果,即“正确答案”。
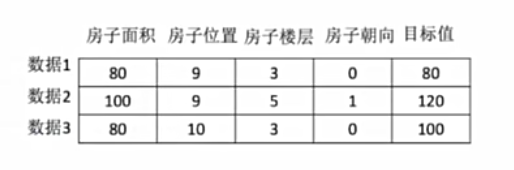
每条数据被成为一条样本。
1.2 机器学习算法简单分类
我们可以根据是否有目标值分类:
监督学习:
分类问题:
目标值是类别,如区分猫和狗的图片。
回归问题:
目标值是连续性的数据,如根据房屋的属性信息预测房屋的价格。
无监督学习:
无目标值,如根据人物的各个属性信息进行分析,将其聚类,无标准答案。
建立的模型又可以根据是否有参数大致分为两类:
非参数化模型:
依赖数据本身,预测时需访问全部数据。
如 KNN(一般用于监督学习)。
参数化模型:
通过优化参数拟合数据,可泛化到新样本。
如线性/Softmax回归、神经网络。
1.3 机器学习的开发流程
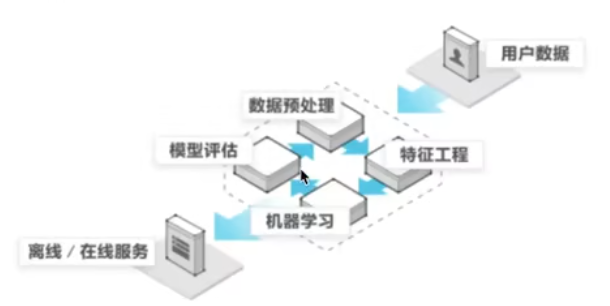
用户数据:原始输入信息,通常是未经处理的样本或记录,作为机器学习流程的起点。
数据预处理:清洗、转换和规范化原始数据,使其适合后续分析和建模。
特征工程:从数据中提取或构造关键特征,以提升模型对目标问题的表达能力。
机器学习:算法从数据中自动学习规律,生成预测或决策模型。
模型评估:通过指标(如准确率、召回率)测试模型性能,验证其泛化能力。
离线/在线服务:离线指批量处理数据(如训练模型),在线指实时响应请求(如API预测)。
2. 非参数化模型:KNN
K最近邻(K-Nearest Neighbors) 是一种基于距离的监督学习算法,其核心逻辑是:“相似的输入会有相似的输出”。
通过计算新样本与训练数据的距离,找到最近的K个邻居,根据这些邻居的类别或值进行预测。
比如我们要解决以下问题:图中存在两种狼群A、B(分别用圆形、正方形表示),现在新加入一只狼,其爪印位置已经确定,请问如何判断它属于哪只狼群?
(1) 计算距离
图中网格背景表示特征空间,每个点的位置由其特征值决定(如二维坐标)。
计算目标点(爪印)与其他点的距离(常用欧氏距离):d=(x1−x2)^2+(y1−y2^)^2
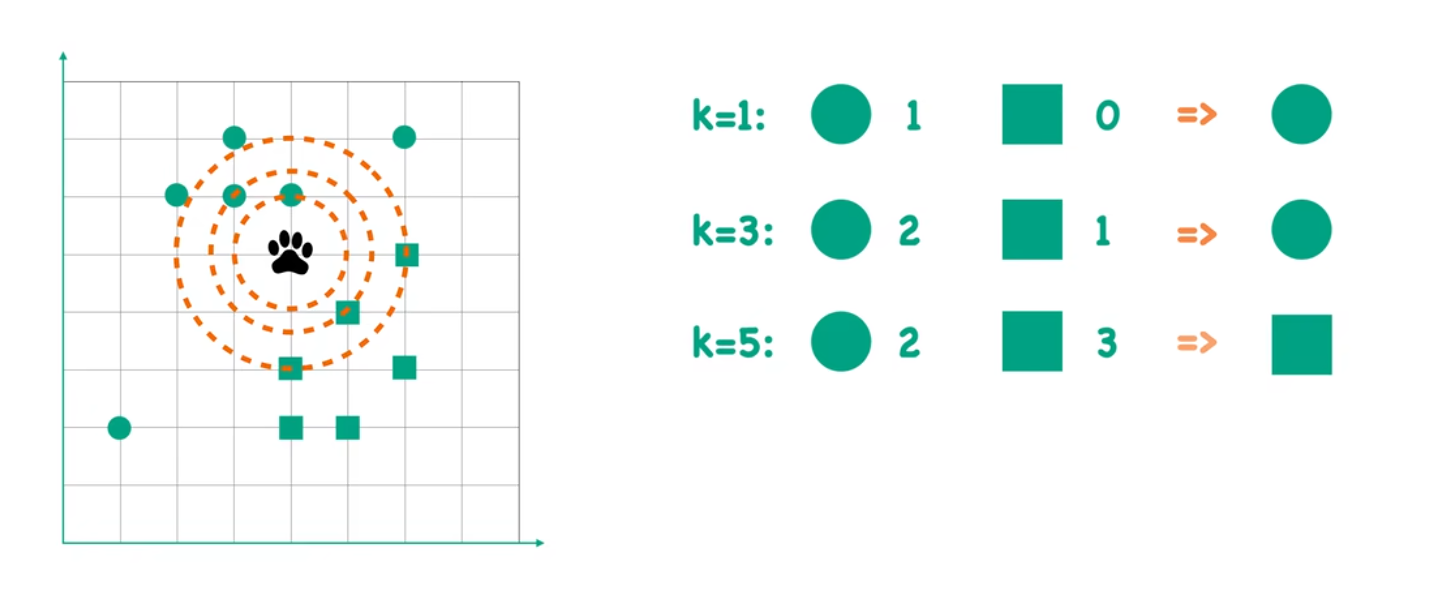
(2) 选择K值
K 是用户定义的邻居数量,直接影响结果:
K=1:只考虑最近的1个邻居(图中绿色方形,类别0)。
K=3:考虑最近的3个邻居(2个类别2 + 1个类别1 → 投票结果为类别2)。
K=5:考虑最近的5个邻居(2个类别2 + 3个类别3 → 投票结果为类别3)。
(3) 决策规则
分类任务:多数投票(如图中示例)。
回归任务:取K个邻居目标值的平均值。
3. 参数化模型
3.1 线性回归
回归是能为自变量与因变量之间关系建模的一类方法。在机器学习领域中大多数通常与预测有关。
线性回归是最简单并且最流行的一种方法。
假如一个样本中,其因变量 y ,只受一个因素影响,我们可以把数据进行回归分析,拟合为 y = wx + b;
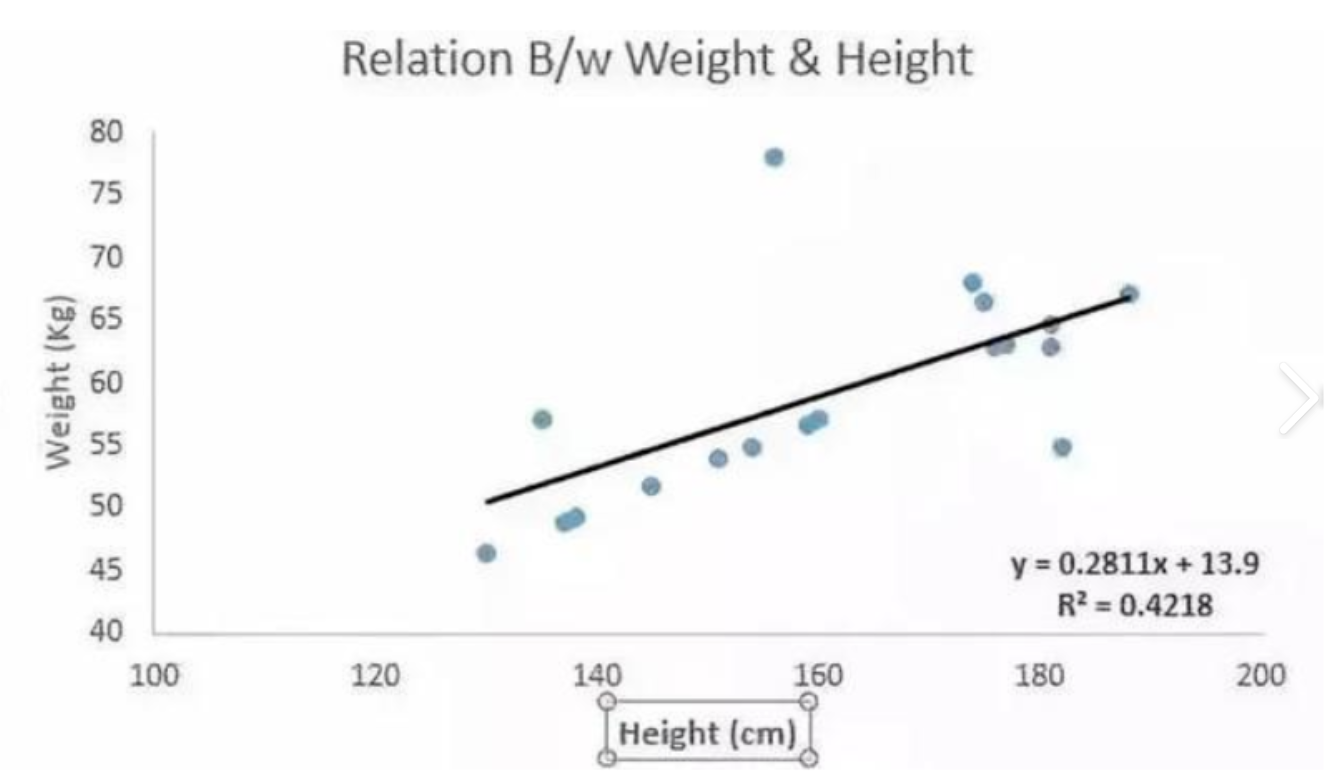
假如一个样本中,其因变量 y,受 d 个因素影响,我们将预测结果 y^(通常使用“尖角”符号表示 𝑦 的估计值)表示为:
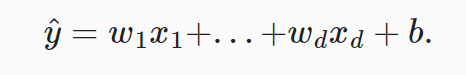
用线性代数的矩阵乘法方式,可以表示为:
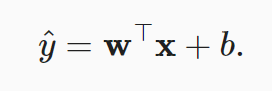
在上述公式中,向量 x 对应于单个数据样本的特征。而拓展到 n 个样本,将向量 x 可以拓展成矩阵 X(n行d列,每一行是一个样本,每一列是一种特征),那么预测值也可以用一个向量 y 表示:
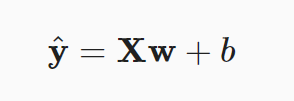
不过,既然我们是预测值,那我们的预测值和实际值一定是有误差的。 损失函数能够量化目标的实际值与预测值之间的差距。以下是一种损失函数:
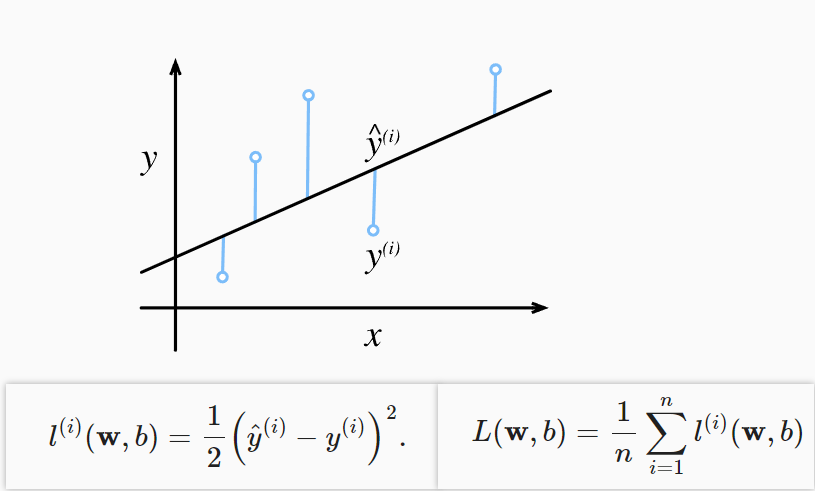
在训练模型时,我们希望寻找一组参数(𝑤∗,𝑏∗), 这组参数能最小化在所有训练样本上的总损失。
线性回归模型存在解析解,可以通过最小化 || y - Xw ||^2 来获得解析解。
我们也可以将线性模型看作一个最简单的神经网络:
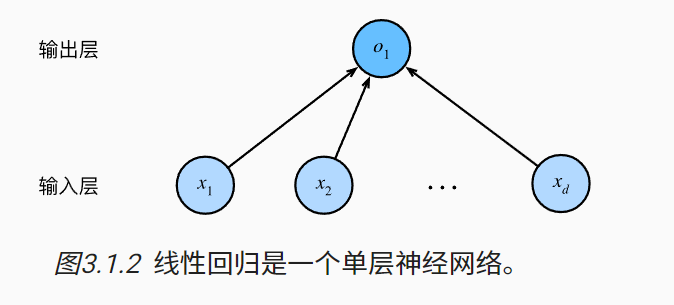
如上图的神经网络中,输入为𝑥1,…,𝑥𝑑, 因此输入层中的输入数为𝑑。 网络的输出为𝑜1,因此输出层中的输出数是1。 需要注意的是,输入值都是已经给定的,并且只有一个计算神经元。 由于模型重点在发生计算的地方,所以通常我们在计算层数时不考虑输入层。
我们可以将线性回归模型视为仅由单个人工神经元组成的神经网络,或称为单层神经网络。
import random
import torch
from d2l import torch as d2l
# 3.2.1 生成数据集
def synthetic_data(w, b, num_examples): # @save
"""生成y=Xw+b+噪声"""
X = torch.normal(0, 1, (num_examples, len(w)))
y = torch.matmul(X, w) + b
y += torch.normal(0, 0.01, y.shape)
return X, y.reshape((-1, 1))
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)
# 查看第一个样本
print('features:', features[0], '\nlabel:', labels[0])
# 可视化数据
d2l.set_figsize()
d2l.plt.scatter(features[:, 1].detach().numpy(), labels.detach().numpy(), 1)
d2l.plt.show()
# 3.2.2 读取数据集
def data_iter(batch_size, features, labels):
num_examples = len(features)
indices = list(range(num_examples))
random.shuffle(indices)
for i in range(0, num_examples, batch_size):
batch_indices = torch.tensor(indices[i: min(i + batch_size, num_examples)])
yield features[batch_indices], labels[batch_indices]
# 3.2.3 初始化模型参数
w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# 3.2.4 定义模型
def linreg(X, w, b): # @save
"""线性回归模型"""
return torch.matmul(X, w) + b
# 3.2.5 定义损失函数
def squared_loss(y_hat, y): # @save
"""均方损失"""
return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2
# 3.2.6 定义优化算法
def sgd(params, lr, batch_size): # @save
"""小批量随机梯度下降"""
with torch.no_grad():
for param in params:
param -= lr * param.grad / batch_size
param.grad.zero_()
# 3.2.7 训练
lr = 0.03
num_epochs = 3
batch_size = 10
net = linreg
loss = squared_loss
for epoch in range(num_epochs):
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y) # 计算小批量损失
l.sum().backward() # 反向传播计算梯度
sgd([w, b], lr, batch_size) # 更新参数
with torch.no_grad():
train_l = loss(net(features, w, b), labels)
print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
# 评估参数估计误差
print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')输出类似如下:
features: tensor([-0.9877, -0.1583])
label: tensor([2.7550])
epoch 1, loss 0.039296
epoch 2, loss 0.000146
epoch 3, loss 0.000051
w的估计误差: tensor([ 0.0010, -0.0013], grad_fn=<SubBackward0>)
b的估计误差: tensor([0.0002], grad_fn=<RsubBackward1>)
Process finished with exit code 03.2 Softmax 回归
分类会关注两个问题:
我们只对样本的“硬性”类别感兴趣,即属于哪个类别;
我们希望得到“软性”类别,即得到属于每个类别的概率。
在机器学习领域中,我们更关注软性类别的模型,即“概率”。这样我们就可以将线性回归扩展了。
自变量(输入):假设每次输入是一个2×2的灰度图像。 我们可以用一个标量表示每个像素值,每个图像对应四个特征𝑥1,𝑥2,𝑥3,𝑥4。
因变量(输出):假设每个图像属于类别“猫”“鸡”和“狗”中的一个。在我们的例子中,标签𝑦将是一个三维向量, 其中(1,0,0)对应于“猫”、(0,1,0)对应于“鸡”、(0,0,1)对应于“狗”。我们管这种方式叫做 one-hot 编码。
为了估计所有可能类别的条件概率,我们需要一个有多个输出的模型,每个类别对应一个输出。
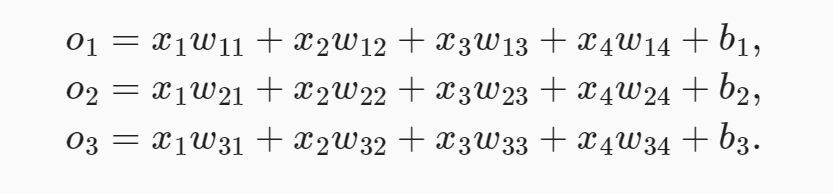
我们把这个模型用神经网络表示如下:
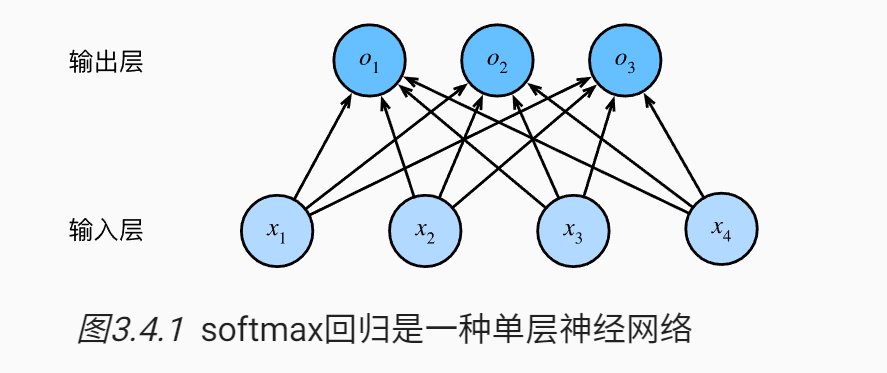
现在,我们得到了一个向量 o,但是我们需要计算的是概率,需要通过一种算法让每个元素的和为1,并且每个元素都必须为非负数。
这种算法就是 Softmax 公式。它让原始的输出转换成了概率分布。

现在我们拿到了最终的概率向量 p。
如同线性回归,Softmax 也有损失函数,即负对数似然损失函数。(即交叉熵损失)
在训练模型时,我们需要让损失函数的值最小。损失函数的目的在让模型对真实类别的预测概率 p_k 尽可能接近 1。


听说字节的算法岗喜欢手撕交叉熵,还直接用 numpy 手撕?不活了吧
3.3 多层感知机 MLP
我们在前两个模型中,可以模拟线性的模型了。
那如何模拟非线性模型呢?我们可以加入一个隐藏层:
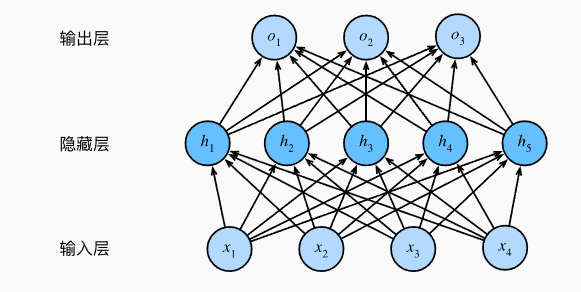
在MLP中,每一层后引入非线性激活函数 σ(如ReLU),打破线性叠加性。以下公式以两层为例,f(x) 就是向量 o:
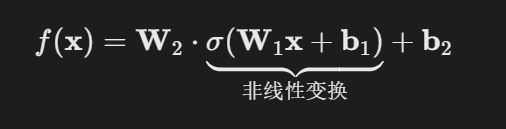
若 σ 为非线性函数(如ReLU: σ(z)=max(0,z)),则 f(x) 不再是输入 x 的线性函数。
通过复合非线性函数,模型可学习输入的分段线性或平滑非线性映射。
运用通用近似定理,通过使用更深(而不是更广)的网络,我们可以更容易地逼近许多函数。
3.4 卷积神经网络 CNN
这里建议去看一下视频,一下子就明白了:https://www.bilibili.com/video/BV1MsrmY4Edi
比如我们有一个图片,像素是 6 * 6 。 0表示黑色, 1表示白色,那么它属于数字 0 ~ 9 的概率分别是多少?
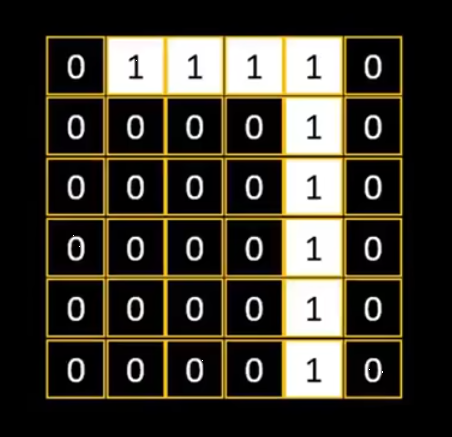
3.4.1 提取图片特征(卷积层)
在这个流程中,我们需要使用卷积核(特征过滤器),用于提取图片特征。
例如,我们定义两个 3 * 3 的卷积核,来表示图片的垂直特征和水平特征:
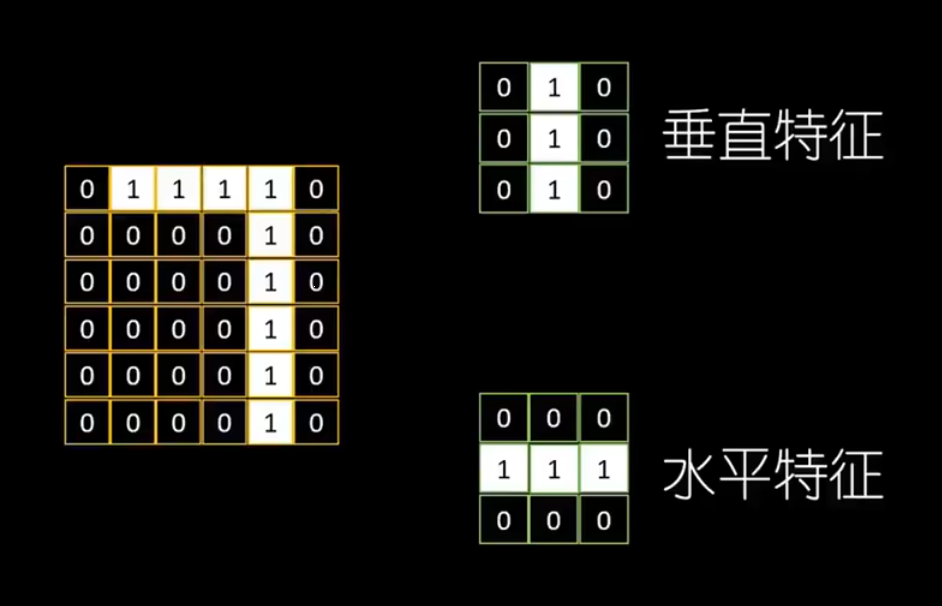
在提取特征的计算上,我们需要按顺序提取原始图片中 3 * 3 的像素区域,再将其每个像素单元依次和卷积核内相对应的像素值相乘,再求和。然后把结果记录在新的 4 * 4 像素图中:
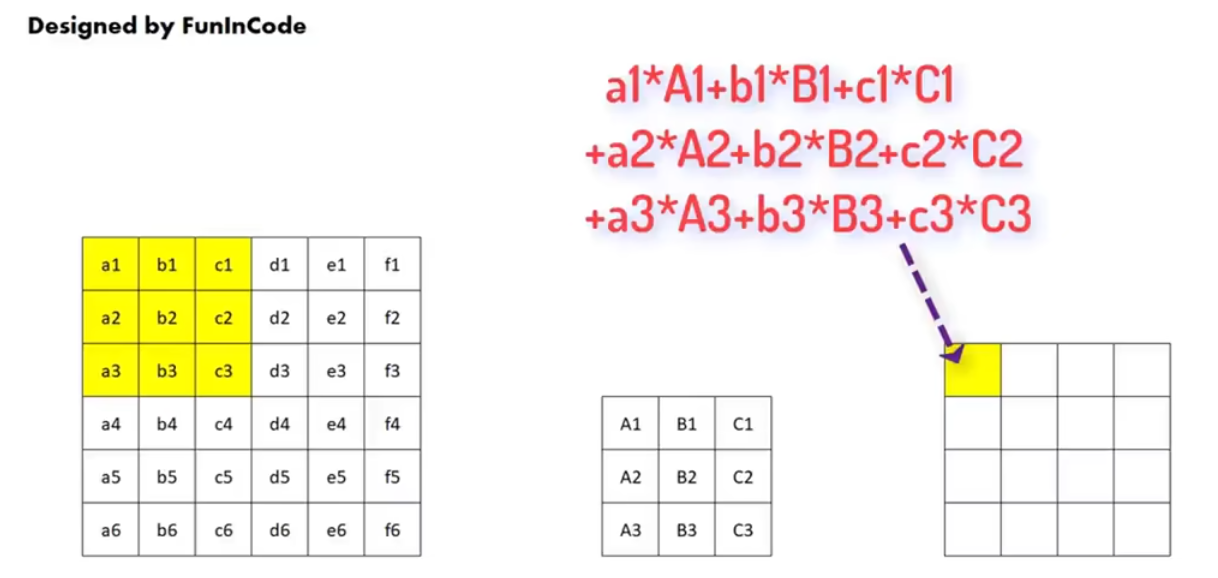
计算过程示例如下,会发现原图中提取的区域和特征越相近,新像素图(特征图)该位置的值越大:
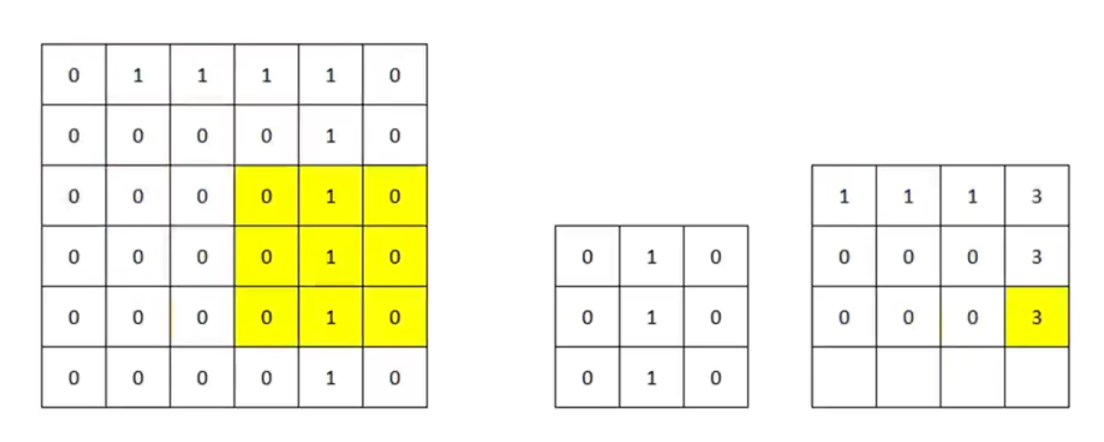
我们可以在特征图中,根据像素值的大小设定颜色的深浅以供直观查看:
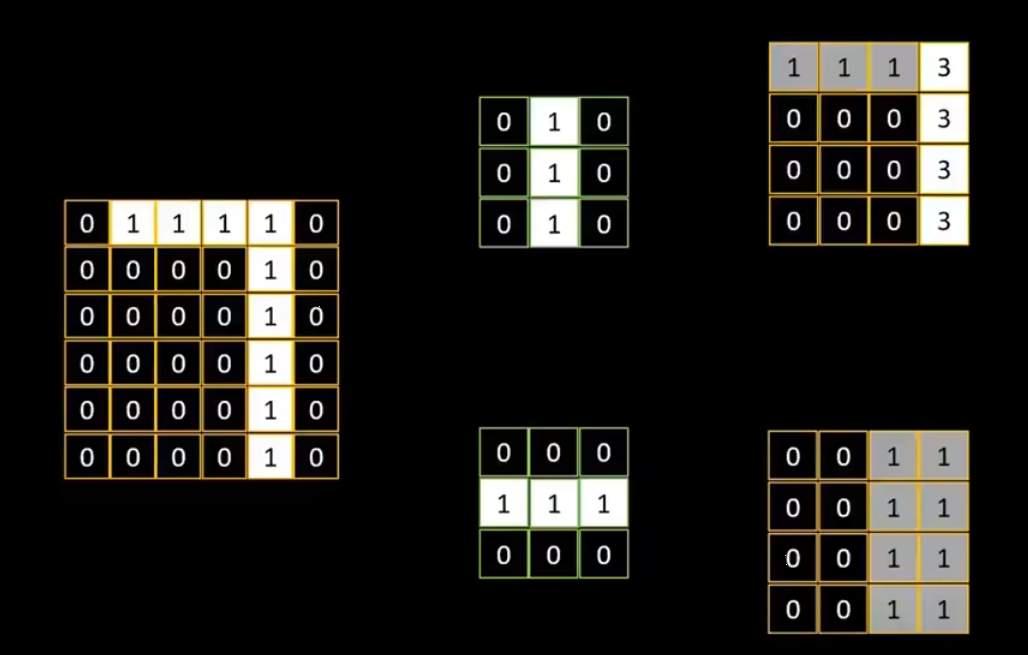
这里我们发现,原始图片 7 的垂直部分特征被很好地提取了出来,但是水平部分特征没有被提取出来。
这是因为在刚才的计算当中,像素图从原来的 6 * 6 被降维成了 4 * 4 ,边缘的特征丢失了。
为了解决边缘特征的提取问题,我们会使用一种被称为 “Padding” 的扩充方法,将原始的 6 * 6 图像先扩充成 8 * 8 ,扩充部分的像素值均设为 0。这样特征图也是 6 * 6 ,我们就能看到垂直和水平特征都得到了完美提取:

有些时候,我们会发现特征值会有负数,这里还需要一层 ReLU 激活来去掉负数响应。
3.4.2 最大池化
这个步骤的目的是将图片中的数据进一步压缩,仅反应特征图中“最突出”的特点。
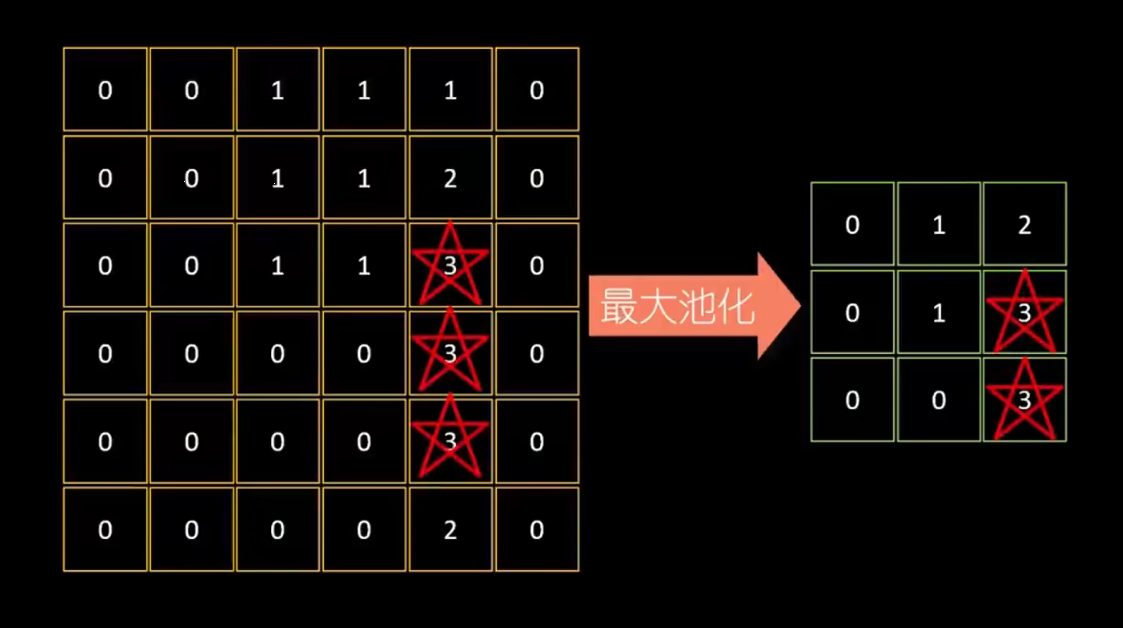
我们将 6 * 6 的特征图用 2 * 2 的网格分割成 3 * 3 的部分,然后提取每个部分中的最大值,放在最大池化后的 3 * 3 网格中。
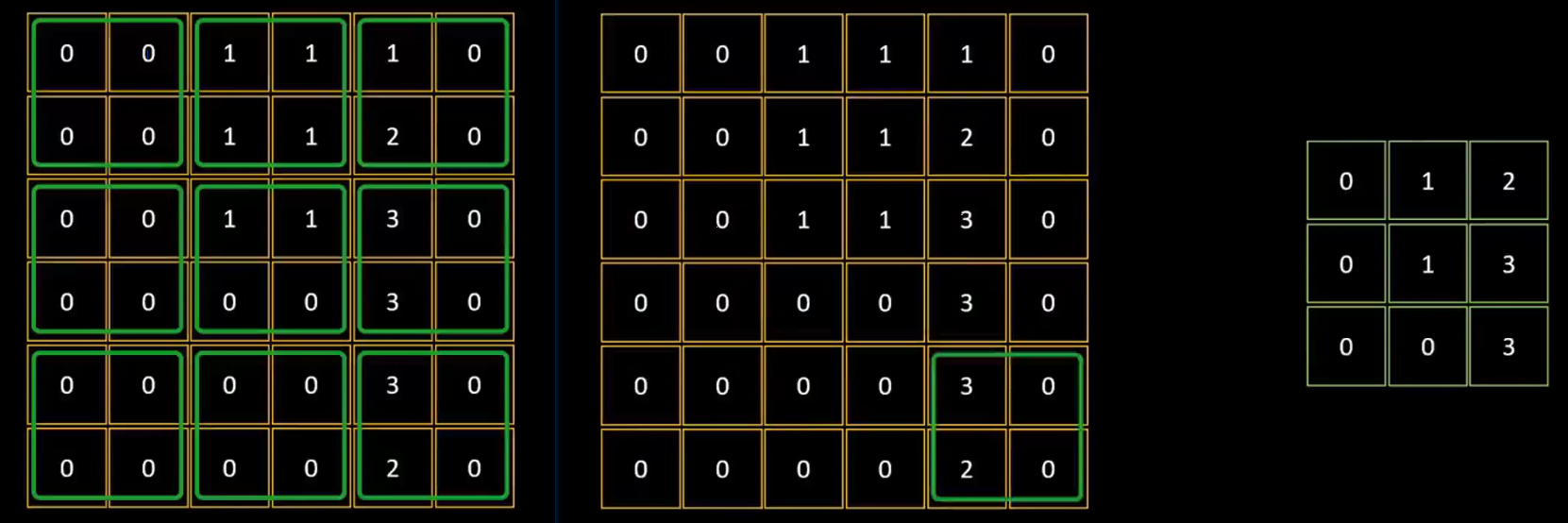
池化后的数据保留了原始数据中最精华的特征部分。
3.4.3 扁平化处理
我们把池化后的数据进行扁平化处理,把两个 3 * 3 的像素图叠加,转化成 1 维的数据“条”。
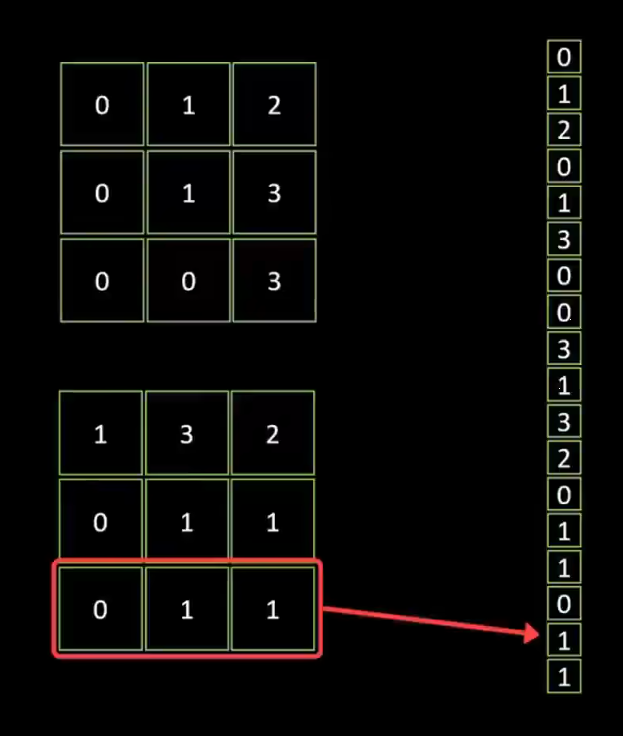
我们将数据条录入到后面的全连接隐藏层,最终产生输出结果。
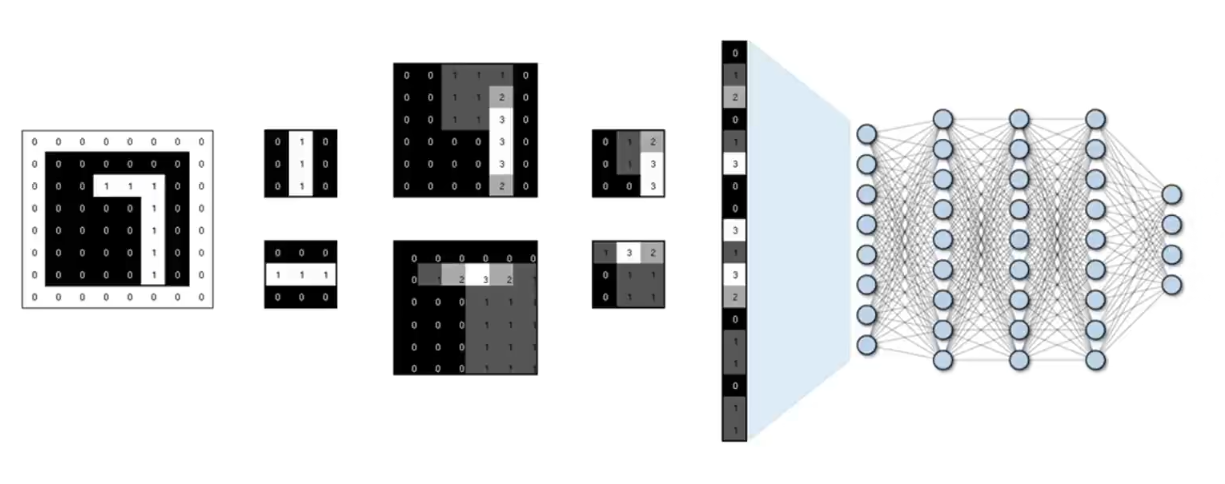
最后的输出层可以使用 Softmax 函数判断它属于 0~9 哪个数字的概率。
3.4.4 完整流程的数学表达
上述提到的每个步骤与CNN组件的对应关系如下:
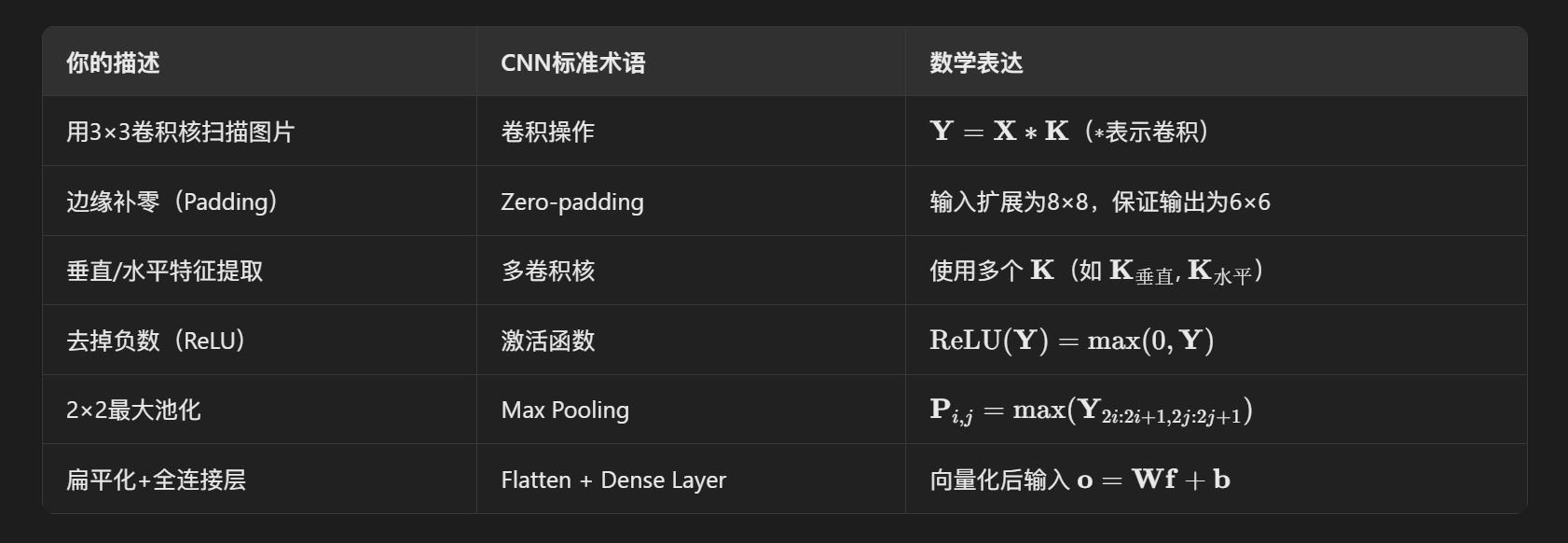
3.4.5 CNN 的核心特性
局部连接性:
每个输出仅依赖输入的3×3局部区域(而非全连接)。
减少计算量,聚焦局部模式(如图像的边缘、纹理)。
权重共享:
同一卷积核在不同位置参数相同(如垂直检测器扫描全图),降低参数量(避免过拟合)。
保证特征检测的位置无关性(无论猫在图像中心还是角落,都能检测)。
平移等变性:
输入平移 → 输出相应平移。
符合图像数据的物理规律(物体移动不影响其类别)。
3.5 神经网络的优化
神经网络的优化是指通过调整网络的参数(如权重和偏置)来最小化损失函数的过程。
目标是找到最优的参数。
以下是神经网络优化的几个关键方面:
3.5.1 损失函数
损失函数(Loss Function)用于衡量神经网络预测值与真实值之间的差异。它是优化目标的具体数学表达。常见的损失函数包括:
均方误差(MSE):用于回归问题,计算预测值与真实值之间的平方差的均值。
交叉熵损失(Cross-Entropy Loss):用于分类问题,衡量预测概率分布与真实分布的差异。
我们要优化的目标就是尽可能最小化这个损失函数。
3.5.2 解析解与梯度下降
解析解:对于某些简单模型(如线性回归),可以通过数学公式直接求出最优参数(如最小二乘法)。但对于神经网络,由于模型复杂且非线性,通常无法直接求解解析解。
梯度下降(Gradient Descent):一种迭代优化方法,通过沿着损失函数的负梯度方向逐步更新参数以最小化损失。参数更新公式:

梯度下降的变体:
随机梯度下降(SGD):每次使用一个样本计算梯度,速度快但波动大。
批量梯度下降(BGD):使用全部样本计算梯度,稳定但计算成本高。
小批量梯度下降(Mini-batch GD):折中方案,每次使用一个小批量样本。
3.5.3 BP 算法
反向传播(Backpropagation, BP)是神经网络训练的核心算法,用于高效计算损失函数对每一层参数的梯度。步骤如下:
前向传播:输入数据通过网络逐层计算,得到预测输出。
计算损失:比较预测输出与真实值,计算损失函数值。
反向传播:
从输出层开始,计算损失函数对输出的梯度。
通过链式法则(Chain Rule)将梯度逐层反向传播,计算每一层的权重和偏置的梯度。

参数更新:使用梯度下降或其他优化算法更新参数。
神经网络的优化依赖于:
选择合适的损失函数以匹配任务类型(如分类或回归)。
使用梯度下降及其变体迭代更新参数。
通过反向传播算法高效计算梯度,结合优化器(如 SGD、Adam)加速收敛。
4. PyTorch 实现
4.1 PyTorch Tensor 简介
4.1.1 NumPy 数组简介
NumPy (Numerical Python) 是 Python 中用于对数组进行高性能科学计算的基础库。
NumPy 的核心由 C 语言编写,其操作是向量化的,无需通过循环来进行计算,因此速度和内存上面都有优势。
import numpy as np我们可以用 NumPy 创建一个数组或矩阵(矩阵就是二维数组):
# 从列表创建
a = np.array([1, 2, 3]) # 一维数组
b = np.array([[1, 2], [3, 4]]) # 二维数组
# 特殊数组创建
# 默认情况下,NumPy 数组的元素类型是 float64(浮点数)。
zeros = np.zeros((2, 3)) # 全零数组
ones = np.ones((2, 2)) # 全一数组
eye = np.eye(3) # 单位矩阵每个数组都可以获得它的属性:
arr = np.array([[1, 2, 3], [4, 5, 6]])
print(arr.ndim) # 维度数 → 2
print(arr.shape) # 形状 → (2, 3)
print(arr.size) # 元素总数 → 6
print(arr.dtype) # 数据类型 → int64两个数组可以进行一些数学运算,以最简单的两个一维数组为例:
p我们也可以使用一些函数对 NumPy 数组做一些统计与变换。
arr = np.array([[1, 2], [3, 4]])
print(np.sum(arr)) # 总和 → 10
print(np.mean(arr)) # 平均值 → 2.5
print(np.max(arr)) # 最大值 → 4
print(np.std(arr)) # 标准差 → 1.118
# 形状变换
print(arr.reshape(4, 1)) # 改变形状
print(arr.flatten()) # 展平为一维 → [1,2,3,4]
# 转置
print(arr.T) # [[1,3],[2,4]]4.1.2 PyTorch Tensor 简介
PyTorch 是一个基于 Python 的科学计算库,主要针对深度学习研究。
在深入了解机器学习与深度学习前,我们先了解一下张量(Tensor)这个数据结构。
张量是 PyTorch 中最基本的数据结构,类似于 NumPy 的 ndarray,但可以在 GPU 上加速计算。
import torch
# 从列表创建
x = torch.tensor([1, 2, 3])
print(x) # 控制台输出 tensor([1, 2, 3])类似之前的 NumPy,我们可以直接通过 torch 库的各种函数创建张量:
# 创建全零张量
zeros = torch.zeros(2, 3) # 2行3列
# 创建全一张量
ones = torch.ones(2, 3)
# 创建随机张量
rand = torch.rand(2, 3) # 均匀分布[0,1)
randn = torch.randn(2, 3) # 标准正态分布
# 从NumPy数组创建
import numpy as np
numpy_array = np.array([1, 2, 3])
tensor_from_numpy = torch.from_numpy(numpy_array)对张量进行一些数学运算:
# 数学运算
a = torch.tensor([1, 2, 3])
b = torch.tensor([4, 5, 6])
print(a + b) # 逐元素相加
print(torch.add(a, b)) # 同上
print(a * b) # 逐元素相乘
print(torch.matmul(a, b)) # 点积对张量进行一些形状上的操作:
# 张量形状
x = torch.rand(2, 3)
print(x.size()) # torch.Size([2, 3])
# 改变形状
y = x.view(3, 2) # 不改变数据,只改变视图
z = x.reshape(3, 2) # 类似view,但更灵活4.1.3 KNN 的 PyTorch 实现
import torch
import matplotlib.pyplot as plt
class KNN:
def __init__(self, k=3):
self.k = k
def fit(self, X, y):
self.X_train = torch.tensor(X, dtype=torch.float32)
self.y_train = torch.tensor(y, dtype=torch.long)
def predict(self, X):
X = torch.tensor(X, dtype=torch.float32)
distances = torch.cdist(X, self.X_train) # 计算距离矩阵
_, indices = torch.topk(distances, self.k, largest=False) # 找到最近的k个点
neighbor_labels = self.y_train[indices]
# 投票决定分类 统计k个邻居中圆/方块的数量
predictions = torch.mode(neighbor_labels, dim=1).values
return predictions.numpy()
# 示例数据(根据图片中的布局模拟)
# 假设:绿色圆点=类别0,绿色方块=类别1
X = torch.tensor([
[1.0, 2.0], [1.5, 1.8], [2.0, 1.5], # 类别0的点
[2.5, 2.0], [3.0, 1.8], [3.5, 1.5], # 类别1的点
[2.0, 2.8], [1.8, 3.0], [2.2, 3.2] # 更多类别0的点
])
y = torch.tensor([0, 0, 0, 1, 1, 1, 0, 0, 0])
# 测试点(中心爪印)
test_point = torch.tensor([[2.0, 2.0]])
# 不同k值的预测
for k in [1, 3, 5]:
knn = KNN(k=k)
knn.fit(X, y)
pred = knn.predict(test_point)
print(f"k={k}: 预测类别 → {pred[0]}")
# 可视化(类似图片效果)
plt.figure(figsize=(10, 5))
plt.scatter(X[:6, 0], X[:6, 1], c=['green'] * 3 + ['orange'] * 3, marker='o', s=100, label='类别0')
plt.scatter(X[6:, 0], X[6:, 1], c=['green'] * 3, marker='s', s=100, label='类别1')
plt.scatter(test_point[0, 0], test_point[0, 1], c='red', marker='*', s=200, label='测试点')
# 绘制k=3的决策圈
circle = plt.Circle((2.0, 2.0), 1.2, color='gray', fill=False, linestyle='--')
plt.gca().add_patch(circle)
plt.text(2.0, 0.8, f'k=3时包含{3}个邻居', ha='center')
plt.legend()
plt.title("KNN分类示例 (PyTorch实现)")
plt.grid(True)
plt.show()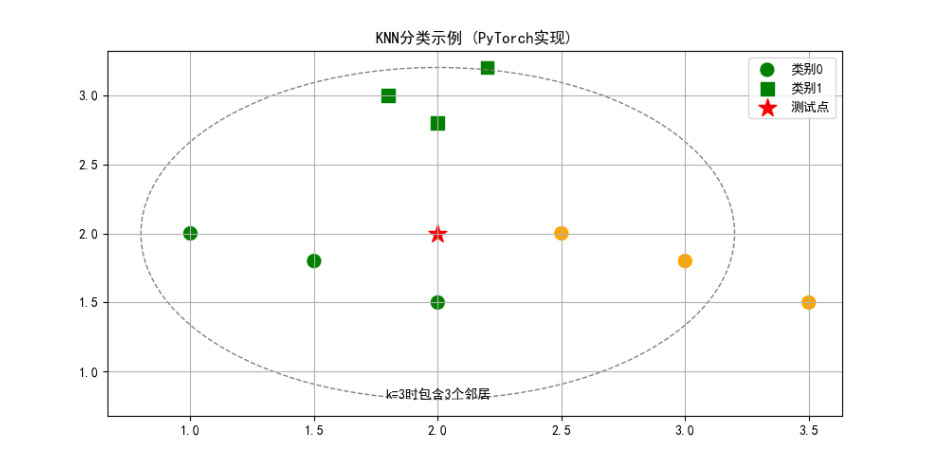
k=1: 预测类别 → 0
k=3: 预测类别 → 0
k=5: 预测类别 → 04.1.4 PyTorch 自动微分简介
PyTorch 还可以做一些微积分计算的工作。我们只需要在一个 tensor 实例调用 backward() 即可。
这里贴一下关于导数的基本概念:

PyTorch 是这样 y = x^2 在 x = 3 处的导数的:
import torch
# 1. 创建一个张量,并告诉PyTorch要计算它的导数
x = torch.tensor(3.0, requires_grad=True)
# 2. 定义计算过程(就像写数学公式)
y = x ** 2
# 3. 自动计算导数
y.backward()
# 4. 查看x的导数值
print(x.grad) # 输出:tensor(6.)然后,再回顾一下多变量函数中梯度的基本概念:

PyTorch 可以计算梯度:
import torch
# 定义需要计算梯度的变量
x = torch.tensor(1.0, requires_grad=True)
y = torch.tensor(2.0, requires_grad=True)
# 定义函数
z = 2*x + 3*y # z = 2 * 1 + 3 * 2 = 8
# 自动计算梯度
z.backward()
# 查看梯度
print(x.grad) # dz/dx = 2 → tensor(2.)
print(y.grad) # dz/dy = 3 → tensor(3.)4.2 机器学习建模基本流程
我们以最基本的线性回归为例梳理一下机器学习建模的基本流程。
4.2.1 数据准备
首先,我们要生成我们的数据集:
目的:创建或加载用于训练和测试的数据。
代码实现:
使用
synthetic_data生成人工数据集,其中X是特征矩阵,y是标签(真实值)。数据生成公式:
y = X @ w + b + 噪声(模拟真实场景的噪声)。
# 生成人工数据集 返回特征矩阵 features 和标签 labels
def synthetic_data(w, b, num_examples): # @save
"""生成y=Xw+b+噪声"""
X = torch.normal(0, 1, (num_examples, len(w)))
y = torch.matmul(X, w) + b
y += torch.normal(0, 0.01, y.shape)
return X, y.reshape((-1, 1))
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)然后我们需要读取数据集,进行一些数据的预处理:
目的:将数据划分为小批量,支持随机梯度下降(SGD)。
代码实现:
data_iter函数对数据随机打乱顺序,并按batch_size分批返回特征和标签。关键操作:
random.shuffle保证每轮训练的样本顺序随机,避免模型学习到顺序偏差。
def data_iter(batch_size, features, labels):
num_examples = len(features)
indices = list(range(num_examples))
random.shuffle(indices)
for i in range(0, num_examples, batch_size):
batch_indices = torch.tensor(indices[i: min(i + batch_size, num_examples)])
yield features[batch_indices], labels[batch_indices]4.2.2 模型定义
我们定义我们需要拟合的线性回归模型。
目的:描述输入特征如何映射到预测输出(即前向传播)。
代码实现:
linreg函数实现线性回归:y_hat = X @ w + b。(y_hat 就是 y^)模型结构决定了学习任务的性质(此处是线性模型)。
def linreg(X, w, b): # @save
"""线性回归模型"""
return torch.matmul(X, w) + b然后我们来初始化一个可学习的参数,我们后续要优化它。
目的:为模型的可学习参数(如权重
w和偏置b)赋初值。代码实现:
w从正态分布采样,b初始化为 0。设置
requires_grad=True以启用自动求导(PyTorch 特性)。
w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)4.2.3 损失函数
目的:量化预测值
y_hat与真实值y的差异,指导参数优化。代码实现:
squared_loss使用均方误差(MSE)的一半(方便求导后系数为1)。
def squared_loss(y_hat, y): # @save
"""均方损失"""
return (y_hat - y.reshape(y_hat.shape)) ** 2 / 24.2.4 优化算法
目的:根据损失函数的梯度更新模型参数。
代码实现:
sgd实现小批量随机梯度下降:参数更新公式:
param -= lr * param.grad / batch_size(梯度均值)。torch.no_grad()上下文禁用梯度计算以提升性能。手动清零梯度(
grad.zero_()),避免梯度累积。
def sgd(params, lr, batch_size): # @save
"""小批量随机梯度下降"""
with torch.no_grad():
for param in params:
param -= lr * param.grad / batch_size
param.grad.zero_()4.2.5 训练循环
目的:通过多轮迭代优化模型参数。
代码实现:
外层循环:
num_epochs控制训练轮数。内层循环:遍历每个小批量数据:
前向计算损失
l = loss(net(X, w, b), y)。反向传播
l.sum().backward()(损失求和后求梯度)。调用
sgd更新参数。
监控:每轮结束后计算全体数据的平均损失,观察收敛情况。
lr = 0.03
num_epochs = 3
batch_size = 10
net = linreg
loss = squared_loss
for epoch in range(num_epochs):
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y) # 计算小批量损失
l.sum().backward() # 反向传播计算梯度
sgd([w, b], lr, batch_size) # 更新参数
with torch.no_grad():
train_l = loss(net(features, w, b), labels)
print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')4.2.6 评估模型
目的:验证模型学到的参数是否接近真实值(或测试集性能)。
代码实现:
比较估计的
w和b与生成数据时使用的真实值true_w和true_b。输出参数误差(此处是合成数据,真实值已知)。
# 评估参数估计误差
print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')4.3 PyTorch nn 模块
PyTorch 的 nn(torch.nn)模块是 PyTorch 中用于构建神经网络的核心模块,它提供了各种层(Layers)、损失函数(Loss Functions)和优化器(Optimizers)的预定义实现,使得构建和训练神经网络变得更加简单和高效。
4.3.1 神经网络模块的基类
nn.Module 是所有神经网络模块的基类,自定义网络必须继承它,并实现 forward() 方法。
比如我们要自定义一个简单的全连接网络:
import torch
import torch.nn as nn
class MyNet(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(10, 5) # 输入维度 10,输出维度 5
self.fc2 = nn.Linear(5, 1) # 输入维度 5,输出维度 1
def forward(self, x):
x = torch.relu(self.fc1(x)) # 第一层 + ReLU 激活
x = self.fc2(x) # 第二层(无激活)
return x
model = MyNet()
print(model)输出:
MyNet(
(fc1): Linear(in_features=10, out_features=5, bias=True)
(fc2): Linear(in_features=5, out_features=1, bias=True)
)4.3.2 常用层 Layers
PyTorch 提供了多种预定义的层,可以直接在模型中使用:
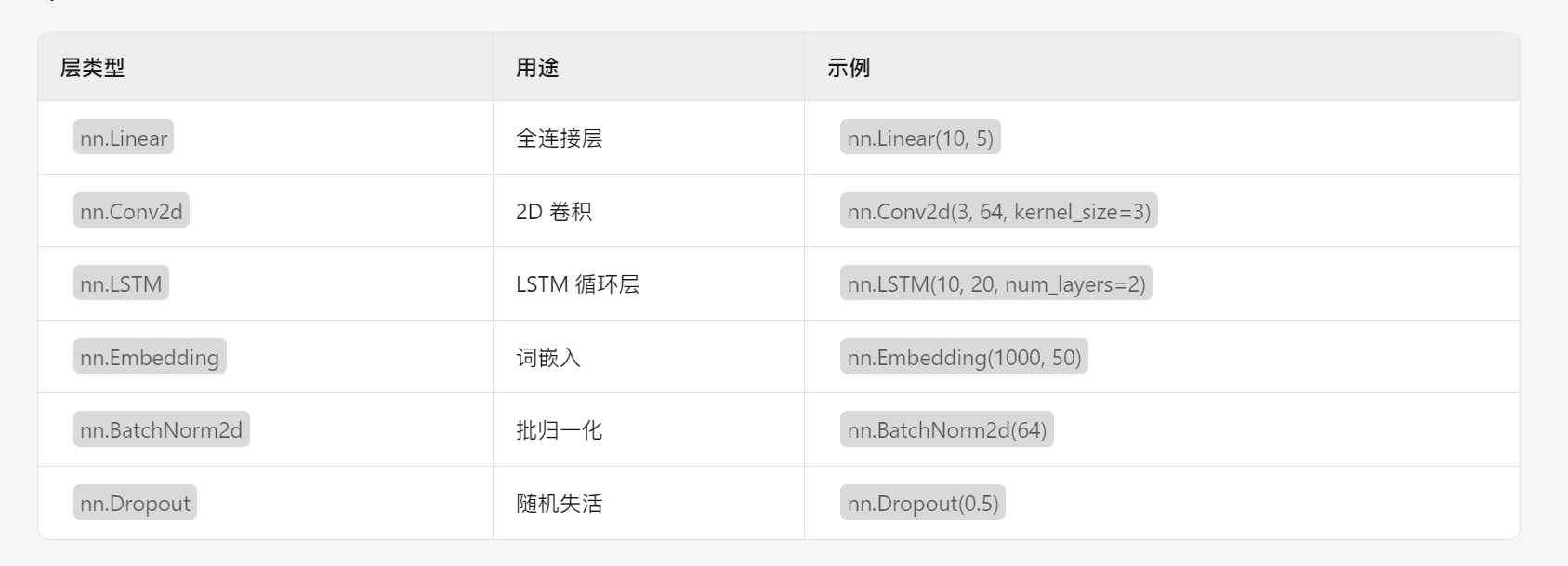
4.3.3 损失函数
PyTorch 提供了多种损失函数,用于训练神经网络:
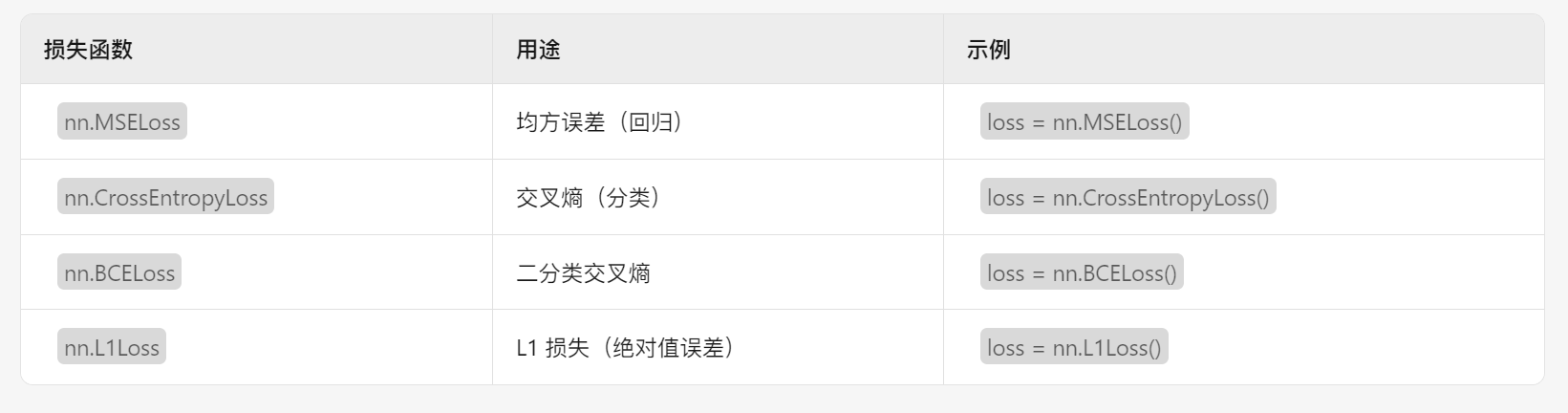
示例:
criterion = nn.MSELoss()
output = model(input_data)
loss = criterion(output, target)
loss.backward() # 反向传播4.3.4 优化算法
PyTorch 提供了多种优化算法,用于更新模型参数:

optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
for epoch in range(100):
optimizer.zero_grad() # 清空梯度
output = model(input_data)
loss = criterion(output, target)
loss.backward() # 反向传播
optimizer.step() # 更新参数参考
【黑马程序员3天快速入门python机器学习】 https://www.bilibili.com/video/BV1nt411r7tj/?p=4&share_source=copy_web&vd_source=0acc90ba529bf1b28fdeb3351912e2f2
动手学深度学习(PyTorch版)
【卷积神经网络(CNN)到底卷了啥?8分钟带你快速了解!】 https://www.bilibili.com/video/BV1MsrmY4Edi/?share_source=copy_web&vd_source=0acc90ba529bf1b28fdeb3351912e2f2
腾讯元宝